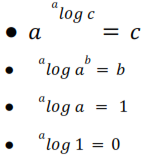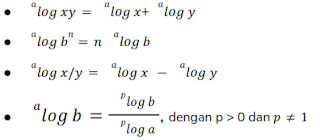Grafik, Persamaan, dan Pertidaksamaan Eksponen dan Logaritma

Sinjai Blog - Asslamu'alaikum wr.wb. kembali lagi bersama admin di blog edukatif dan kreatif. Pada postingan kali ini, kita akan belajar apa itu Grafik, Persamaan, dan Pertidaksamaan Eksponen dan Logaritma. Materi pada postingan kali ini merupakan materi untuk SMA kelas 10 dan sangat bermanfaat sekali bagi adik-adik yang ingin lebih paham lagi dengan Materi Eksponen dan Logaritma.

Pertama yang perlu kita ketahui adalah pengertian dari Grafik, Eksponen, dan Logaritma.

Grafik adalah sebuah representasi grafis dari data. Data yang diwakili dibentuk oleh simbol-simbol, seperti batang dalam grafik batang, garis-garis dalam sebuah grafik garis, atau irisan dalam grafik pai. Sebuah grafik dapat mewakili bentuk tabel numerik data, fungsi, atau beberapa jenis struktur kualitatif yang memberikan informasi yang berbeda.

Eksponen adalah suatu bentuk perkalian dengan bilangan yang sama kemudian di ulang-ulang, yaa semacam perkalian yang diulang-ulang gitu deh. Eksponen bisa juga kita kenal sebagai bilangan berpangkat.

Logaritma adalah suatu invers atau kebalikan dari pemangkatan (eksponen) yang digunakan untuk menentukan besar pangkat dari suatu bilangan pokok.

a. Eksponen

Bentuk 𝑎ⁿ disebut sebagai bentuk eksponensial atau perpangkatan, dengan a disebut basis atau bilangan pokok dan n adalah pangkat atau eksponen. Sifat-sifat yang berlaku dalam bilangan berpangkat rasional diantaranya adalah sebagai berikut :

b. Logaritma

Secara Umum didefinisikan sebagai berikut :

𝑎^b = c ⇔ b = ^𝑎 log c dengan 𝑎 > 0 𝑎 ≠ 1

berikut adalah sifat-sifat dari logaritma :

c. Persamaan Eksponen dan Pertidaksamaan Eksponen

Jika 𝑎^{f (x)} = 1, f (x) = 0, 𝑎 > 0, 𝑎 ≠ 1

Jika 𝑎^{f (x)} = 𝑎^p, f (x) = p, 𝑎 > 0, 𝑎 ≠ 1

Jika 𝑎^{f (x)} = 𝑎^{g (x)}, f (x) = g (x), 𝑎 > 0, 𝑎 ≠ 1

Jika 𝑎^{f (x)} = b^{g (x)}, 𝑎 = b , 𝑎 > 0, 𝑎 ≠ 1, b > 0 , b ≠ 1

Untuk Pertidaksamaan eksponen menggunakan konsep yang sama seperti persamaan eksponen hanya membedakan tanda, misalnya :

 𝑎^{f (x) <} 𝑎^p , maka f (x) < p, untuk 𝑎 > 0 , 𝑎 ≠ 1

d. Persamaan Logaritma dan Pertidaksamaan Logaritma

Untuk 𝑎 > 0 dan 𝑎 ≠ 1, serta f (x) > 0 dan g (x) > 0, diperoleh :

^𝑎 log f (x) = ^𝑎log b, f (x) = b

^𝑎log f (x) = ^blog f (x), f (x) = 1

^𝑎log f (x) = ^𝑎log g (x), f (x) = g (x)

^{f (x)} log g (x) = ^{f (x)}log h (x), g (x) = h (x)

Untuk pertidaksamaan logaritma sama sajaseperti persamaan logaritma, konsepnya hanya berbeda tanda saja, misalkan :

 ^𝑎 log f (x) > ^𝑎log b,  maka f (x) > b untuk a > 0 dan 𝑎 ≠ 1

nah itu dia materi eksponen dan logaritma untuk kali ini. materi ini merupakan materi awal dalam mempelajari mate-matika di bangku kelas 10 SMA. semoga dengan materi ini dapat membantu adik-adik dalam belajar dan meraih prestasi setinggi-tinggi nya.